A. Mousavi, G. Dasarathy, R. G. Baraniuk, “DeepCodec: Adaptive Sensing and Recovery via Deep Convolutional Neural Networks,” arXiv:1707.03386, July 2017.
We develop a novel computational sensing framework for sensing and recovering structured signals called DeepCodec. When trained on a set of representative signals, our framework learns to take undersampled measurements and recover signals from them using a deep convolutional neural network. In other words, it learns a transformation from the original signals to a near-optimal number of undersampled measurements and the inverse transformation from measurements to signals. This is in contrast to conventional compressive sensing (CS) systems that use random linear measurements and convex optimization or iterative algorithms for signal recovery. We compare our new framework with ℓ1-minimization from the phase transition point of view and demonstrate that it outperforms ℓ1-minimization in the regions of phase transition plot where ℓ1-minimization cannot recover the exact solution. In addition, we experimentally demonstrate how learning measurements enhances recovery performance, speeds up training, and reduces the number of parameters to learn.
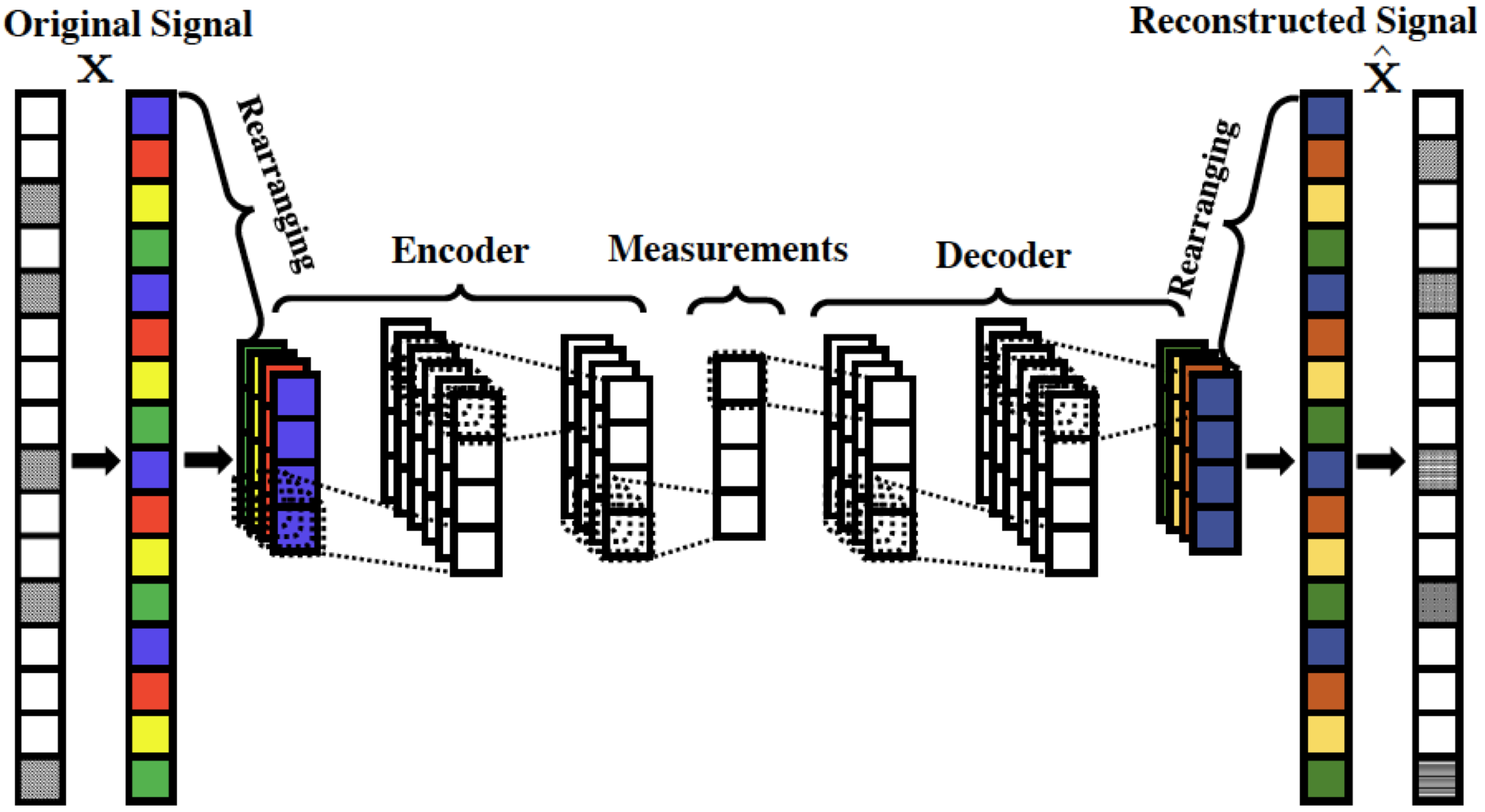
DeepCodec learns a transformation from signals x to measurement vectors y and an approximate inverse transformation from measurement vectors y to signals x using a deep convolutional network that consists of convolutional and sub-pixel convolution layers.

Recovery comparison of DeepCodec vs. LASSO (with optimal regularization parameter).