A. Patel, T. Nguyen, and R. G. Baraniuk, "A Probabilistic Theory of Deep Learning," arXiv preprint, arxiv.org/abs/1504.00641, 2 April 2015. Updated version from NIPS 2016.
Abstract: A grand challenge in machine learning is the development of computational algorithms that match or outperform humans in perceptual inference tasks such as visual object and speech recognition. The key factor complicating such tasks is the presence of numerous nuisance variables, for instance, the unknown object position, orientation, and scale in object recognition or the unknown voice pronunciation, pitch, and speed in speech recognition. Recently, a new breed of deep learning algorithms have emerged for high-nuisance inference tasks; they are constructed from many layers of alternating linear and nonlinear processing units and are trained using large-scale algorithms and massive amounts of training data. The recent success of deep learning systems is impressive -- they now routinely yield pattern recognition systems with near- or super-human capabilities -- but a fundamental question remains: Why do they work? Intuitions abound, but a coherent framework for understanding, analyzing, and synthesizing deep learning architectures has remained elusive.
We answer this question by developing a new probabilistic framework for deep learning based on a Bayesian generative probabilistic model that explicitly captures variation due to nuisance variables. The graphical structure of the model enables it to be learned from data using classical expectation-maximization techniques. Furthermore, by relaxing the generative model to a discriminative one, we can recover two of the current leading deep learning systems, deep convolutional neural networks (DCNs) and random decision forests (RDFs), providing insights into their successes and shortcomings as well as a principled route to their improvement.
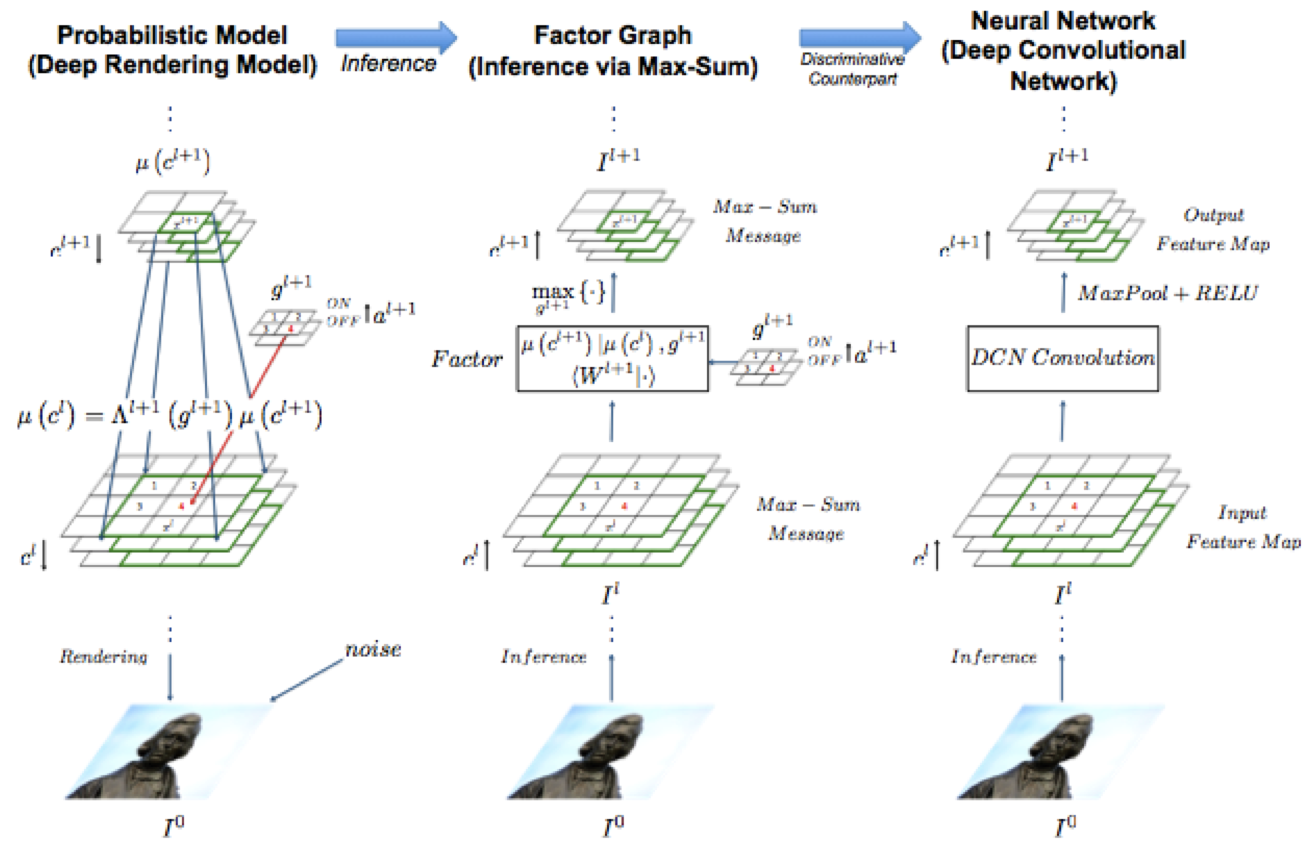
The figure below illustrates an example of a mapping from our Deep Rendering Model (DRM) to its factor graph to a Deep Convolutional Network (DCN) at one level of abstraction. The factor graph representation of the DRM supports efficient inference algorithms such as max-sum message passing. The computational algorithm that implements the max-sum message passing algorithm matches that of a DCN.