T. Goldstein, C. Studer, and R. G. Baraniuk, “A Field Guide to Forward-Backward Splitting with a FASTA Implementation,” arXiv preprint, arxiv.org/abs/1411.3406, December 2014
Non-differentiable and constrained optimization play a key role in machine learning, signal and image processing, communications, and beyond. For high-dimensional minimization problems involving large datasets or many unknowns, the forward-backward splitting (FBS) method (also called the proximal gradient method) provides a simple, practical solver. Despite its apparently simplicity, the performance of the forward-backward splitting is highly sensitive to implementation details. Our research explores FBS with a special emphasis on practical implementation concerns and considering issues such as stepsize selection, acceleration, stopping conditions, and initialization. Our new solver FASTA (short for Fast Adaptive Shrinkage/Thresholding Algorithm) incorporates many variations of forward-backward splitting and provides a simple interface for applying FBS to a broad range of problems.
Software for FASTA is available here
Example: "Two Moons" data set for testing machine learning (classification) algorithms
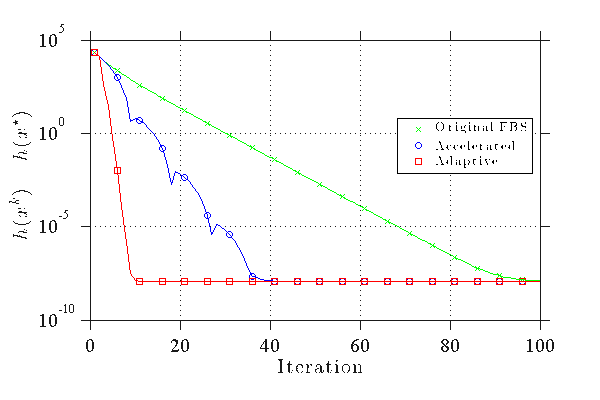
 Convergence of FASTA (red) on Two Moons versus more conventional forward-backward splitting (FBS) techniques
Convergence of FASTA (red) on Two Moons versus more conventional forward-backward splitting (FBS) techniques