A. Lan, D. Vats, A. Waters, and R. G. Baraniuk, "Mathematical Language Processing: Automatic Grading and Feedback for Open Response Mathematical Questions,"
ACM Conference on Learning at Scale, Vancouver, March 2015.
Abstract: While computer and communication technologies have provided effective means to scale up many aspects of education, the submission and grading of assessments such as homework assignments and tests remains a weak link. In this paper, we study the problem of automatically grading the kinds of open response mathematical questions that figure prominently in STEM (science, technology, engineering, and mathematics) courses. Our data-driven framework for mathematical language processing (MLP) leverages solution data from a large number of learners to evaluate the correctness of their solutions, assign partial-credit scores, and provide feedback to each learner on the likely locations of any errors.
MLP takes inspiration from the success of natural language processing for text data and comprises three main steps. First, we convert each solution to an open response mathematical question into a series of numerical features. Second, we cluster the features from several solutions to uncover the structures of correct, partially correct, and incorrect solutions. We develop two different clustering approaches, one that leverages
generic clustering algorithms and one based on Bayesian nonparametrics. Third, we automatically grade the remaining (potentially large number of) solutions based on their assigned cluster and one instructor-provided grade per cluster. As a bonus, we can track the cluster assignment of each step of a multistep solution and determine when it departs from a cluster of correct solutions, which enables us to indicate the likely locations of errors to learners. We test and validate MLP on real-world MOOC data to demonstrate how it can substantially reduce the human effort required in large-scale educational platforms.
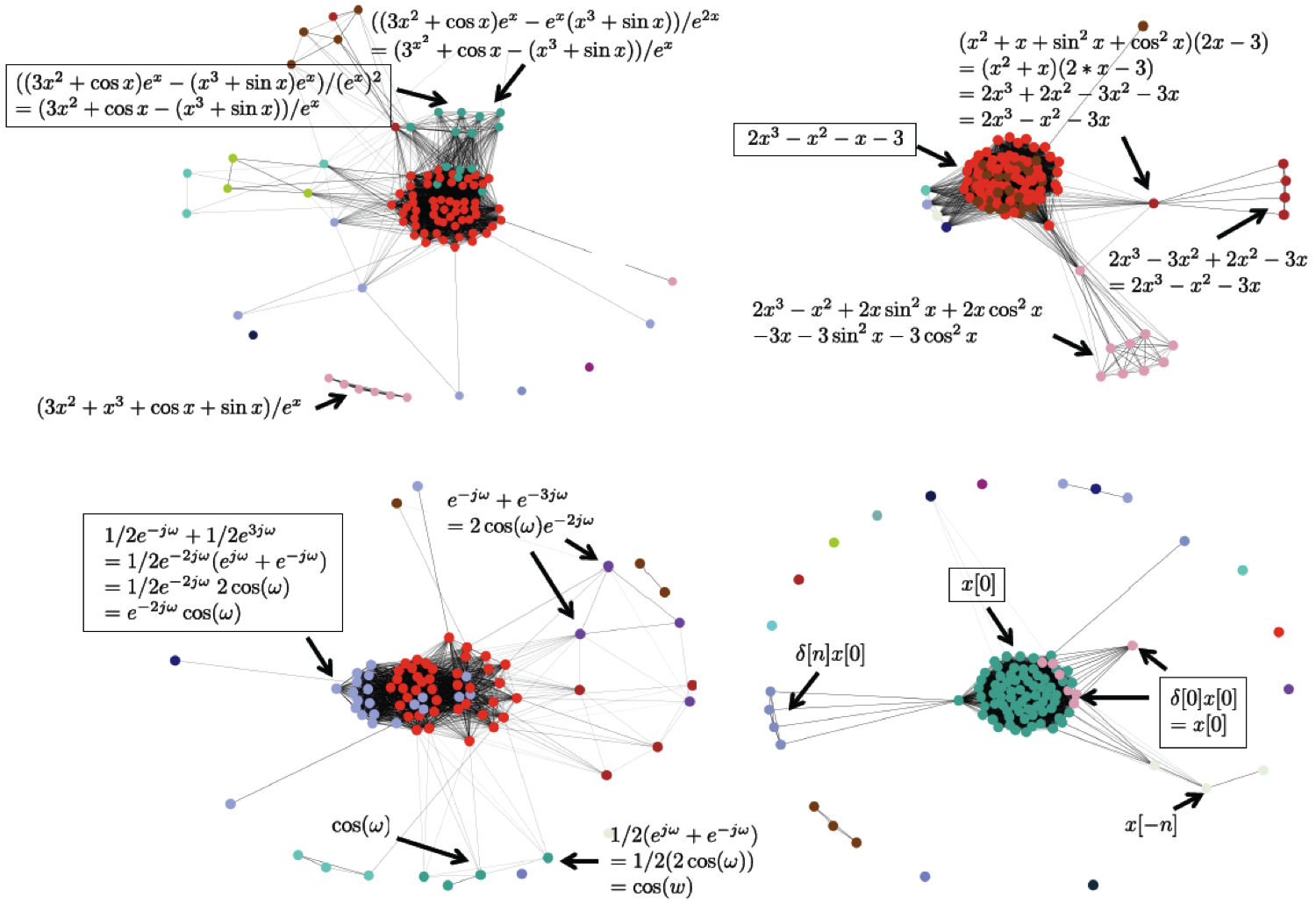
The figure below illustrates the clusters obtained by MLP to the solutions of 100 learners to four different mathematical questions (two from algebra and two from Fourier analysis). Each node corresponds to a solution. Nodes with the same color correspond to solutions that are estimated to be in the same cluster. The thickness of the edge between two solutions is proportional to their similarity score. Boxed solutions are correct; others have varying degrees of correctness.
The examples below demonstrate the generation of real-time feedback generation by MLP while learners enter their solutions. After each expression, we compute both the probability that the learner’s solution belongs to a cluster that does not have full credit (3 points) and the learner’s expected grade. An alert is generated when the expected credit is less than full credit.
